数据编码

假设字长(word size)为 $w$,也即数据的位数，则二进制向十进制的转换分别是：

无符号数：
$$
B2U(X)=\sum_{i=0}^{w-1}x_i\cdot2^i
$$
有符号数：
$$
B2T(X)=-x_{w-1}\cdot2^{w-1}+\sum_{i=0}^{w-2}x_i\cdot2^{i}
$$

左移：x向左移动k位，丢弃最高的k位，在右端补k个0；

逻辑右移：在左端补k个0

算术右移：在左端补k个最高有效位的值

PS：移位操作优先级低于±，

无符号数编码定义：
$$
B2U_w(x)=\sum_{i=0}^{w-1}x_i2^i
$$
原码：正数是其二进制本身；负数是符号位为1,数值部分取X绝对值的二进制。

最高位是符号位，用来确定剩下的位是应该取负权还是正权。
$$
B2S_w(x)=(-1)^{x_{w-1}}\cdot(\sum_{i=0}^{w-2}x_i2^i)
$$
补码：正数的补码和原码，反码相同；负数是符号位为1，其它位是原码按位取反，未位加1。（或者说负数的补码是其绝对值反码未位加1）

最高位$x_{w-1}$也称为符号位，其权重为$-2^{w-1}$

$$
B2T_w(x)=-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i
$$

反码：正数的反码和原码相同；负数是符号位为1,其它位是原码取反。

除最高位权为$-(2^{w-1}-1)$而不是$-2^{w-1}$其余和补码一样。
$$
B2O_w(x)=-x_{w-1}(2^{w-1}-1)+\sum_{i=0}^{w-2}x_i2^i
$$

编码	10810（sbyte）	-10810（sbyte）
原码	01101100	11101100
反码	01101100	10010011
补码	01101100	10010100

与 And：A=1 且 B=1 时，A&B = 1
或 Or：A=1 或 B=1 时，A|B = 1
非 Not：A=1 时，~A=0；A=0 时，~A=1
异或 Exclusive-Or(Xor)：A=1 或 B=1 时，A^B = 1；A=1 且 B=1 时，A^B = 0

对应与集合运算则是交集、并集、差集和补集，假设集合 A 是 {0, 3, 5, 6}，集合 B 是 {0, 2, 4, 6}，全集为 {0, 1, 2, 3, 4, 5, 6, 7}那么：

& 交集 Intersection {0, 6}
| 并集 Union {0, 2, 3, 4, 5, 6}
^ 差集 Symmetric difference {2, 3, 4, 5}
~ 补集 Complement {1, 3, 5, 7}

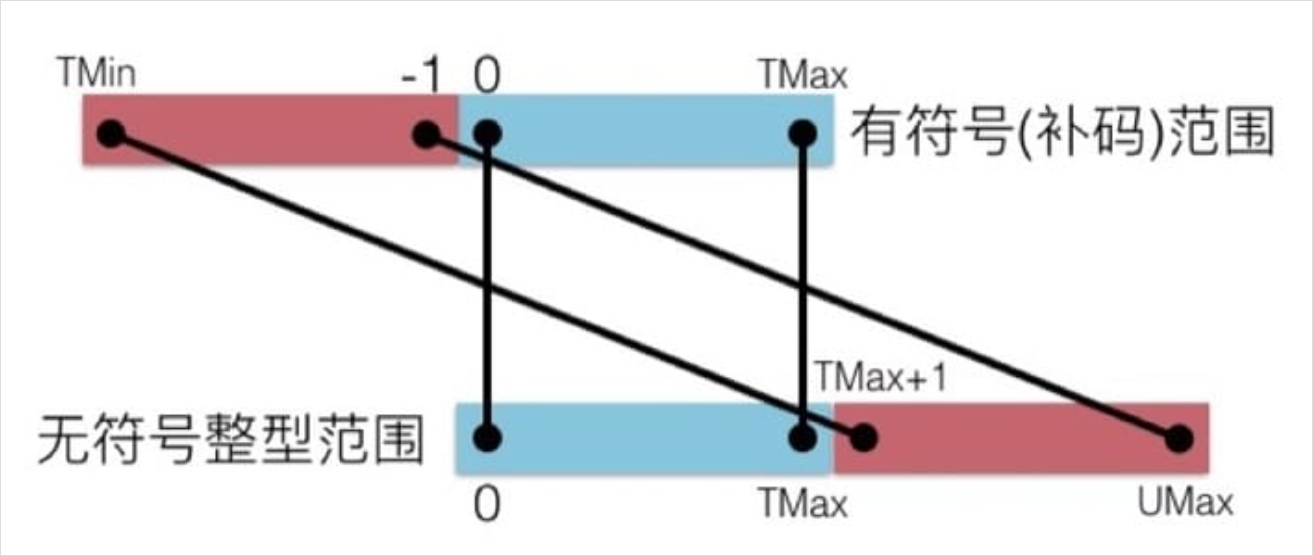
类型转换
我们在数轴上把有符号数和无符号数画出来的话，就能很清晰的看出相对的关系：

在 C 语言中，如果不加关键字限制，默认的整型是有符号的。如果想要无符号数的话，需要在数字后面加 U，例如下面的代码段

1 2	int a_signed_number = -15213; unsigned int a_unsigned_number = 15213U;

在进行有符号和无符号数的互相转换时：

具体每一个字节的值不会改变，改变的是计算机解释当前值的方式
如果一个表达式既包含有符号数也包含无符号数，那么会被隐式转换成无符号数进行比较

表达式	比较对象	求值
0 == 0U	无符号数	1
-1 < 0	有符号数	1
-1 < 0U	无符号数	0*
2147483647 > (-2147483647-1)	有符号数	1
2147483647U < (-2147483647-1)	无符号数	0*
-1 > -2	有符号数	1
(unsigned)-1 > -2	无符号数	1
2147483647 < 2147483648U	无符号数	1
2147483647 > (int)2147483648U	有符号数	1*